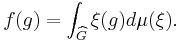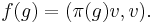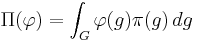Bochner's theorem
In mathematics, Bochner's theorem (named for Salomon Bochner) characterizes the Fourier transform of a positive finite Borel measure on the real line. More generally in harmonic analysis, Bochner's theorem asserts that under Fourier transform a continuous positive definite function on a locally compact abelian group corresponds to a finite positive measure on the Pontryagin dual group.
Contents |
Background
Given a positive finite Borel measure μ on the real line R, the Fourier transform Q of μ is the continuous function
Q is continuous since for a fixed x, the function e-itx is continuous and periodic. The function Q is a positive definite function, i.e. the kernel K(x, y) = Q(y - x) is positive definite; this can be checked via a direct calculation.
The theorem
Bochner's theorem says the converse is true, i.e. every positive definite function Q is the Fourier transform of a positive finite Borel measure. A proof can be sketched as follows.
Let F0(R) be the family of complex valued functions on R with finite support, i.e. f(x) = 0 for all but finitely many x. The positive definite kernel K(x, y) induces a sesquilinear form on F0(R). This in turn results in a Hilbert space
whose typical element is an equivalence class [g]. For a fixed t in R, the "shift operator" Ut defined by (Utg)(x) = g(x - t), for a representative of [g] is unitary. In fact the map
is a strongly continuous representation of the additive group R. By Stone's theorem, there exists a (possibly unbounded) self-adjoint operator A such that
This implies there exists a finite positive Borel measure μ on R where
where e0 is the element in F0(R) defined by e0(m) = 1 if m = 0 and 0 otherwise. Because
the theorem holds.
The theorem for locally compact abelian groups
If G is a locally compact Abelian group with dual group 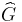 , then any normalized positive definite function f on G is the Fourier transform of a probability measure μ on
, then any normalized positive definite function f on G is the Fourier transform of a probability measure μ on 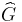 , so that
, so that
In fact continuous unitary representations π of G with a cyclic unit vector v correspond to continuous positive definite functions f on G through the Gelfand–Naimark construction
Each such representation correponds to a continuous non-degenerate *-representation of the convolution algebra L1(G)
and hence, by Fourier transform, of its C* algebra 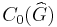 .
.
On the other hand matrix coefficients of non-degenerate continuous *-representations of C0(X) with X a locally compact space, in this case 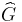 , correspond to probability measures on X.
, correspond to probability measures on X.
Applications
In statistics, one often has to specify a covariance matrix, the rows and columns of which correspond to observations of some phenomenon. The observations are made at points 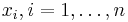 in some space. This matrix is to be a function of the positions of the observations and one usually insists that points which are close to one another have high covariance. One usually specifies that the covariance matrix
in some space. This matrix is to be a function of the positions of the observations and one usually insists that points which are close to one another have high covariance. One usually specifies that the covariance matrix 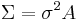 where
where 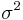 is a scalar and matrix
is a scalar and matrix  is n by n with ones down the main diagonal. Element
is n by n with ones down the main diagonal. Element 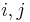 of
of  (corresponding to the correlation between observation i and observation j) is then required to be
(corresponding to the correlation between observation i and observation j) is then required to be 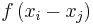 for some function
for some function 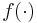 , and because
, and because  must be positive definite,
must be positive definite, 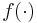 must be a positive definite function. Bochner's theorem shows that
must be a positive definite function. Bochner's theorem shows that 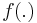 must be the characteristic function of a symmetric PDF.
must be the characteristic function of a symmetric PDF.
See also
References
- Loomis, L. H. (1953), An introduction to abstract harmonic analysis, Van Nostrand
- M. Reed and B. Simon, Methods of Modern Mathematical Physics, vol. II, Academic Press, 1975.
- Rudin, W. (1990), Fourier analysis on groups, Wiley-Interscience, ISBN: 0-471-52364-X
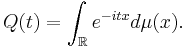

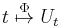
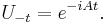
![\langle U_{-t} [e_0], [e_0] \rangle = \int e^{-iAt} d \mu(x) ,](/2012-wikipedia_en_all_nopic_01_2012/I/a63f22ed012843acfc8300665f8f730c.png)
![\langle U_{-t} [e_0], [e_0] \rangle = K(-t,0) = Q(t),](/2012-wikipedia_en_all_nopic_01_2012/I/47ba361fe6214146b7e233d9af90eb9d.png)